Appearance
Table of Contents generated with DocToc
Stack
Conception
A stack is the basic data structure that can be logically thought of as a linear structure.
Insertion and deletion of items at the top of the stack and the operation should obey the rules LIFO(Last In First Out).

Implementation
Each data structure can be implemented by the different method. We can treat stack as a subclass of Array. So we take the array for example here.
js
class Stack {
constructor() {
this.stack = []
}
push(item) {
this.stack.push(item)
}
pop() {
this.stack.pop()
}
peek() {
return this.stack[this.getCount() - 1]
}
getCount() {
return this.stack.length
}
isEmpty() {
return this.getCount() === 0
}
}Application
We choose the NO.20 topic in LeetCode
Our goal is to match the brackets. We can use the features of the stack to implement it.
js
var isValid = function (s) {
let map = {
'(': -1,
')': 1,
'[': -2,
']': 2,
'{': -3,
'}': 3
}
let stack = []
for (let i = 0; i < s.length; i++) {
if (map[s[i]] < 0) {
stack.push(s[i])
} else {
let last = stack.pop()
if (map[last] + map[s[i]] != 0) return false
}
}
if (stack.length > 0) return false
return true
};Queues
concept
A queue is a linear data structure. The insertion takes place at one end while the deletion occurs the other one. And the operation should obey the rules FIFO(First In First Out).

implementation
Here, we'll talk two implementations of the queue: Singly-linked Queue and Circular Queue.
Singly-linked Queue
js
class Queue {
constructor() {
this.queue = []
}
enQueue(item) {
this.queue.push(item)
}
deQueue() {
return this.queue.shift()
}
getHeader() {
return this.queue[0]
}
getLength() {
return this.queue.length
}
isEmpty() {
return this.getLength() === 0
}
}It is an O(n) operation to enqueue in a Singly-linked Queue, while it is an average O(1) in a Circular Queue. So here comes the Circular Queue.
Circular Queue
js
class SqQueue {
constructor(length) {
this.queue = new Array(length + 1)
// head of the queue
this.first = 0
// tail of the queue
this.last = 0
// size of the queue
this.size = 0
}
enQueue(item) {
// the array need to expand if last + 1 is the head
// `% this.queue.length` is to avoid index out of bounds
if (this.first === (this.last + 1) % this.queue.length) {
this.resize(this.getLength() * 2 + 1)
}
this.queue[this.last] = item
this.size++
this.last = (this.last + 1) % this.queue.length
}
deQueue() {
if (this.isEmpty()) {
throw Error('Queue is empty')
}
let r = this.queue[this.first]
this.queue[this.first] = null
this.first = (this.first + 1) % this.queue.length
this.size--
// if the size of queue is too small
// reduce the size half when the real size is quarter of the length and the length is not 2
if (this.size === this.getLength() / 4 && this.getLength() / 2 !== 0) {
this.resize(this.getLength() / 2)
}
return r
}
getHeader() {
if (this.isEmpty()) {
throw Error('Queue is empty')
}
return this.queue[this.first]
}
getLength() {
return this.queue.length - 1
}
isEmpty() {
return this.first === this.last
}
resize(length) {
let q = new Array(length)
for (let i = 0; i < length; i++) {
q[i] = this.queue[(i + this.first) % this.queue.length]
}
this.queue = q
this.first = 0
this.last = this.size
}
}Linked List
Concept
The linked list is a linear data structure and born to be recursive structure. It can fully use the memory of the computer and manage the memory dynamically and flexibly. But Nodes in the linked list must be read in order from the beginning which can be random in the array, and it uses more memory than the array because of the storage used by their pointers.

Implementation
Singly-linked list
javascript
class Node {
constructor(v, next) {
this.value = v
this.next = next
}
}
class LinkList {
constructor() {
// size
this.size = 0
// virtual head
this.dummyNode = new Node(null, null)
}
find(header, index, currentIndex) {
if (index === currentIndex) return header
return this.find(header.next, index, currentIndex + 1)
}
addNode(v, index) {
this.checkIndex(index)
// the next of the node inserted should be previous node'next
// and the previous node's next should point to the node insert,
// except inserted to tail which next is null
let prev = this.find(this.dummyNode, index, 0)
prev.next = new Node(v, prev.next)
this.size++
return prev.next
}
insertNode(v, index) {
return this.addNode(v, index)
}
addToFirst(v) {
return this.addNode(v, 0)
}
addToLast(v) {
return this.addNode(v, this.size)
}
removeNode(index, isLast) {
this.checkIndex(index)
index = isLast ? index - 1 : index
let prev = this.find(this.dummyNode, index, 0)
let node = prev.next
prev.next = node.next
node.next = null
this.size--
return node
}
removeFirstNode() {
return this.removeNode(0)
}
removeLastNode() {
return this.removeNode(this.size, true)
}
checkIndex(index) {
if (index < 0 || index > this.size) throw Error('Index error')
}
getNode(index) {
this.checkIndex(index)
if (this.isEmpty()) return
return this.find(this.dummyNode, index, 0).next
}
isEmpty() {
return this.size === 0
}
getSize() {
return this.size
}
}Tree
Binary Tree
Binary Tree is a common one of the many structures of the tree. And it is born to be recursive.
Binary tree start at a root node and each node consists of two child-nodes at most: left node and right node. The nodes in the bottom are usually called leaf nodes, and when the leaf nodes is full, we call the Full Binary Tree.
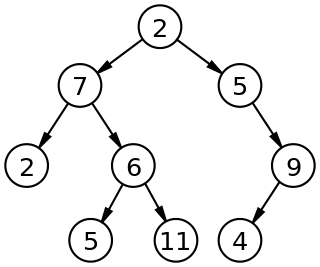
Binary Search Tree
Binary Search Tree (BST) is one of the binary trees, so it has all the features of the binary tree. But different with the binary tree, the value in any node is larger than the values in all nodes in that node's left subtree and smaller than the values in all nodes in that node's right subtree.
This storage method is very suitable for data search. As shown below, when you need to find 6, because the value you need to find is larger than the value of the root node, you only need to find it in the right subtree of the root node, which greatly improves the search efficiency.
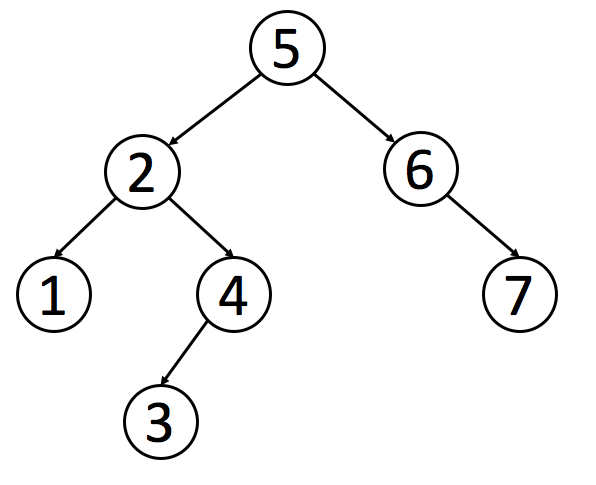
Implementation
js
class Node {
constructor(value) {
this.value = value
this.left = null
this.right = null
}
}
class BST {
constructor() {
this.root = null
this.size = 0
}
getSize() {
return this.size
}
isEmpty() {
return this.size === 0
}
addNode(v) {
this.root = this._addChild(this.root, v)
}
// make comparison to the value of the node when insertion
_addChild(node, v) {
if (!node) {
this.size++
return new Node(v)
}
if (node.value > v) {
node.left = this._addChild(node.left, v)
} else if (node.value < v) {
node.right = this._addChild(node.right, v)
}
return node
}
}Above is the basic implementation of BST, the implementation of traversing tree are as follows.
There are three ways for traversing trees: Preorder Traversal, In order Traversal, PostOrder Traversal. The difference of these ways is the time when to visit the root node. In the process of traversing the tree, each node traverses three times, traversing itself, traversing the left subtree and traversing the right subtree. If you need to implement pre-order traversal, you only need to operate the first time when traversing to the node.
Following are the implementation by recursive, if you want to find the non-recursive, click here
js
// Preorder traversal can be used to print the structure of the tree
// first root then left, and the right is last
traversal() {
this._pre(this.root)
}
_pre(node) {
if (node) {
console.log(node.value)
this._pre(node.left)
this._pre(node.right)
}
}
// Inorder traversal can be used to order
// you can sort the value of BST only by one time of Inorder traversal
// first left , then root and right is last
midTraversal() {
this._mid(this.root)
}
_mid(node) {
if (node) {
this._mid(node.left)
console.log(node.value)
this._mid(node.right)
}
}
// Postorder traversal can be used in the case that you want to
// operate the child node first and then the parent node
// first left, then right and the root is last
backTraversal() {
this._back(this.root)
}
_back(node) {
if (node) {
this._back(node.left)
this._back(node.right)
console.log(node.value)
}
}These three ways belong to Deep First Search. Meanwhile, there is Breadth First Search, which traverse the node layer by layer. We can implement it in the queue.
js
breadthTraversal() {
if (!this.root) return null
let q = new Queue()
// enqueue the root node
q.enQueue(this.root)
// whether the queue is empty, if true, the traverse is finished.
while (!q.isEmpty()) {
// dequeue the head, and whether it has child-node,
// if true, enqueue th left and the right
let n = q.deQueue()
if (n.left) q.enQueue(n.left)
if (n.right) q.enQueue(n.right)
}
}We will introduce how to find the smallest and the biggest in the tree. Because of the feature of the BST, the smallest must be on the left while the biggest is on the right.
js
getMin() {
return this._getMin(this.root).value
}
_getMin(node) {
if (!node.left) return node
return this._getMin(node.left)
}
getMax() {
return this._getMax(this.root).value
}
_getMax(node) {
if (!node.right) return node
return this._getMin(node.right)
}Round up and Round down Since these two operations are opposite, the code is similar, here we'll talk about round down. According to the feature of the BST, the target must be on the left. We only need to traverse the left nodes until the current node is no bigger than the target. And then adjudge if there have right nodes, if do, continue the judgment recursively.
js
floor(v) {
let node = this._floor(this.root, v)
return node ? node.value : null
}
_floor(node, v) {
if (!node) return null
if (node.value === v) return v
// if the current node is bigger than the target, continue
if (node.value > v) {
return this._floor(node.left, v)
}
// whether the current node has the right subtree
let right = this._floor(node.right, v)
if (right) return right
return node
}Rank get the rank of the given value or get the value of the given rank, and these two operations are also similar. We as usual only introduce the operation of the latter. We should retrofit the code to add a property size to each node which indicates how many subnodes a node has, include itself.
js
class Node {
constructor(value) {
this.value = value
this.left = null
this.right = null
// add code
this.size = 1
}
}
// add code
_getSize(node) {
return node ? node.size : 0
}
_addChild(node, v) {
if (!node) {
return new Node(v)
}
if (node.value > v) {
// edit code
node.size++
node.left = this._addChild(node.left, v)
} else if (node.value < v) {
// edit code
node.size++
node.right = this._addChild(node.right, v)
}
return node
}
select(k) {
let node = this._select(this.root, k)
return node ? node.value : null
}
_select(node, k) {
if (!node) return null
// get the size of the node in the left subtree
let size = node.left ? node.left.size : 0
// if size is bigger than k, the target is in the left side
if (size > k) return this._select(node.left, k)
// if the size is smaller than k, the target is in the right side
// there is need to recalculate the k
if (size < k) return this._select(node.right, k - size - 1)
return node
}Here come the most difficult parts in BST: delete nodes, include the following cases:
- the target node has no subtree
- the target node has only one subtree
- the target node has two subtrees
The first and the second is easy to resolve, while the last is a little difficult. So let us implement the simple operation at first: delete the minimum node. It could not appear in the third case, and the operation delete the largest node is opposite, so there is no need to talk.
js
delectMin() {
this.root = this._delectMin(this.root)
console.log(this.root)
}
_delectMin(node) {
// rescursive the left subtree
// if the left subtree is null, check if the right is exist
// if true, take the right subtree in place of the delect node
if ((node != null) & !node.left) return node.right
node.left = this._delectMin(node.left)
// update the size at last
node.size = this._getSize(node.left) + this._getSize(node.right) + 1
return node
}The last, how to delete a random node. T.Hibbard put forward the solution in 1962 which can be used to solve the third case.
In this situation, we should get the descendant node of the current node which is the smallest node in the current node's right subtree and replace the target node by it. And then assign the descendant node with the subtree of the target, and give the right subtree without decent node to the left subtree.
Since the root node is bigger than all the nodes in left subtree, while less than all the nodes in the right subtree. When you want to delete a root node, you need to pick a suitable node to take place, which should bigger than the root node that means it must come from the right subtree. Then the smallest node would be picked with the limit that all the nodes in the right subtree should bigger than the root node.
js
delect(v) {
this.root = this._delect(this.root, v)
}
_delect(node, v) {
if (!node) return null
// if the target is less than the current node, serach in the left subtree
if (node.value < v) {
node.right = this._delect(node.right, v)
} else if (node.value > v) {
// if the target is bigger than the current node, serach in the right subtree
node.left = this._delect(node.left, v)
} else {
// in this case, the target has been found
// check if the node has subtree
// if true, return the subtree, same operation with `_delectMin`
if (!node.left) return node.right
if (!node.right) return node.left
// in this case, the node has both subtree
// get the decendent node of the current node,
// which is the smallest node in the right subtree
let min = this._getMin(node.right)
// delete the smallest after got it
// Then assign the subtree after deleting the node to the smallest node
min.right = this._delectMin(node.right)
// subtree is the same
min.left = node.left
node = min
}
// update size
node.size = this._getSize(node.left) + this._getSize(node.right) + 1
return node
}AVL Tree
Concept
BST is limited in the production because it is not the strict O(log N) and sometimes it will degenerate to a linked list, e.g., insertion of an ascending order number list.
AVL tree improved the BST, the difference between the left subtree height and the right subtree height in each node is less than 1, which can ensure that the time complexity is strict O(log N). Based on this, the insertion and deletion may need to rotate the tree to balance the height.
Implementation
Since improved from the BST, some codes in AVL are repeated, which we will not analysis again.
Four cases are in the node insertion of AVL tree.

As for l-l(left-left), the new node T1 is in the left side of the node X. The tree cannot keep balance by now, so there need to rotate. After rotating, the tree should still obey the rules the mid is bigger than the left and less than the right according to the features of the BST.
before rotating: T1 < X < T2 < Y < T3 < Z < T4, after rotating, the node Y is the root, so we need to add the right subtree of Y to the left of the Z and update the height of the nodes.
The same situation to the r-r, opposite to the l-l, we do not talk more.
As for the l-r, the new node is on the right side of the node X, and we need to rotate twice.
First, rotate the left node to the left, after that the case change to l-l, we can handle it like l-l.
js
class Node {
constructor(value) {
this.value = value
this.left = null
this.right = null
this.height = 1
}
}
class AVL {
constructor() {
this.root = null
}
addNode(v) {
this.root = this._addChild(this.root, v)
}
_addChild(node, v) {
if (!node) {
return new Node(v)
}
if (node.value > v) {
node.left = this._addChild(node.left, v)
} else if (node.value < v) {
node.right = this._addChild(node.right, v)
} else {
node.value = v
}
node.height =
1 + Math.max(this._getHeight(node.left), this._getHeight(node.right))
let factor = this._getBalanceFactor(node)
// when need right-rotate, the height of the left subtree must higher than right
if (factor > 1 && this._getBalanceFactor(node.left) >= 0) {
return this._rightRotate(node)
}
// when need left-rotate, the height of the left subtree must lower than right
if (factor < -1 && this._getBalanceFactor(node.right) <= 0) {
return this._leftRotate(node)
}
// l-r
// left subtree is higher than right,
// and the right subtree of the left subtree of the node
// is higher than the left subtree of the left subtree of the node
if (factor > 1 && this._getBalanceFactor(node.left) < 0) {
node.left = this._leftRotate(node.left)
return this._rightRotate(node)
}
// r-l
// left subtree is lower than right,
// and the right subtree of the right subtree of the node
// is lower than the left subtree of the right subtree of the node
if (factor < -1 && this._getBalanceFactor(node.right) > 0) {
node.right = this._rightRotate(node.right)
return this._leftRotate(node)
}
return node
}
_getHeight(node) {
if (!node) return 0
return node.height
}
_getBalanceFactor(node) {
return this._getHeight(node.left) - this._getHeight(node.right)
}
// right-rotate
// 5 2
// / \ / \
// 2 6 ==> 1 5
// / \ / / \
// 1 3 new 3 6
// /
// new
_rightRotate(node) {
// new root after rotate
let newRoot = node.left
// node need to be moved
let moveNode = newRoot.right
// right node of the node 2 change to node 5
newRoot.right = node
// left node of node 5 change to node 3
node.left = moveNode
// update the height
node.height =
1 + Math.max(this._getHeight(node.left), this._getHeight(node.right))
newRoot.height =
1 +
Math.max(this._getHeight(newRoot.left), this._getHeight(newRoot.right))
return newRoot
}
// left-rotate
// 4 6
// / \ / \
// 2 6 ==> 4 7
// / \ / \ \
// 5 7 2 5 new
// \
// new
_leftRotate(node) {
// new root after rotate
let newRoot = node.right
// node need to be moved
let moveNode = newRoot.left
// left node of the node 6 change to node 4
newRoot.left = node
// right node of the node 4 change to node 5
node.right = moveNode
// update the height
node.height =
1 + Math.max(this._getHeight(node.left), this._getHeight(node.right))
newRoot.height =
1 +
Math.max(this._getHeight(newRoot.left), this._getHeight(newRoot.right))
return newRoot
}
}Trie
Concept
In computer science, a trie, also called digital tree and sometimes radix tree or prefix tree (as prefixes can search them), is a kind of search tree—an ordered tree data structure that is used to store a dynamic set or associative array where the keys are usually strings.
Simply, this data structure is used to search string easily, with the following features:
- the root is on behalf of the empty string, and each node has N links (N is 26 in searching English character), each link represents a character.
- all nodes do not store a character, and only the path store, this is different from other tree structures.
- the character in the path from the root to the random node can combine to the strings corresponding to the node
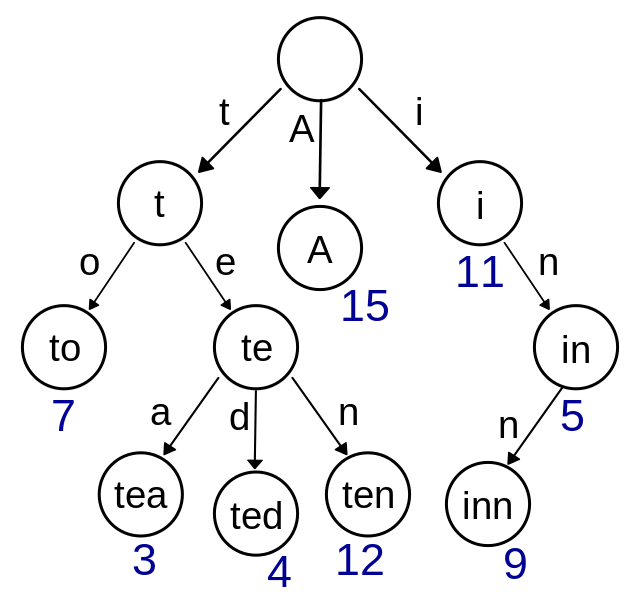
Implementation
Generally, the implementation of the trie is much more simple than others, let's take the English character searching for example.
js
class TrieNode {
constructor() {
// the times of each character travels through the node
this.path = 0
// the amount of the string to the node
this.end = 0
// links
this.next = new Array(26).fill(null)
}
}
class Trie {
constructor() {
// root node, empty string
this.root = new TrieNode()
}
// insert string
insert(str) {
if (!str) return
let node = this.root
for (let i = 0; i < str.length; i++) {
// get the index of the character
let index = str[i].charCodeAt() - 'a'.charCodeAt()
// create if without the index
if (!node.next[index]) {
node.next[index] = new TrieNode()
}
node.path += 1
node = node.next[index]
}
node.end += 1
}
// The number of times the search string appears
search(str) {
if (!str) return
let node = this.root
for (let i = 0; i < str.length; i++) {
let index = str[i].charCodeAt() - 'a'.charCodeAt()
// if the index does node exists, there is no string to be search
if (!node.next[index]) {
return 0
}
node = node.next[index]
}
return node.end
}
// delete the string
delete(str) {
if (!this.search(str)) return
let node = this.root
for (let i = 0; i < str.length; i++) {
let index = str[i].charCodeAt() - 'a'.charCodeAt()
// if the path is 0, this means no string pass
// delete it
if (--node.next[index].path == 0) {
node.next[index] = null
return
}
node = node.next[index]
}
node.end -= 1
}
}Disjoint Set
Concept
Disjoint Set is a special data structure of the tree. Each node in this structure has a parent node, if there is only the current node, then the pointer of the parent node points to itself.
Two important operations are in this structure,
- Find: find the member of the set to which the element belongs, and it can be used to determine whether the two elements belong to the same set
- Union: combine two sets to a new set
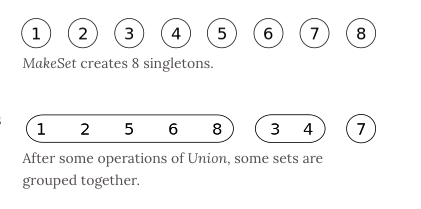
Implementation
js
class DisjointSet {
// init sample
constructor(count) {
// each node's parenet node is iteself when initialization
this.parent = new Array(count)
// record the deepth of the tree to optimize the complexity of query
this.rank = new Array(count)
for (let i = 0; i < count; i++) {
this.parent[i] = i
this.rank[i] = 1
}
}
find(p) {
// check whether the parent node of the current node is itself, if false, means has not found yet
// uglify the path for optimization
// assume the parent node of the current node is A
// mount the current node to the parent node of A to deeply optimize
while (p != this.parent[p]) {
this.parent[p] = this.parent[this.parent[p]]
p = this.parent[p]
}
return p
}
isConnected(p, q) {
return this.find(p) === this.find(q)
}
// combine
union(p, q) {
// find the parent node of the two number
let i = this.find(p)
let j = this.find(q)
if (i === j) return
// compare the deepth of the two trees
// if the deepth is equal, add as you wish
if (this.rank[i] < this.rank[j]) {
this.parent[i] = j
} else if (this.rank[i] > this.rank[j]) {
this.parent[j] = i
} else {
this.parent[i] = j
this.rank[j] += 1
}
}
}Heap
Concept
Heap is usually treated as a tree-based array list.
It is implemented by constructure binary heap, one of the BST. Features are as follows:
- each node either larger or less than all its child-nodes
- heap is always a full-tree
We call the heap Max Binary Heap that its root value is the largest, while the heap with the smallest root value is called Min Binary Heap.
Priority Queue also can be implemented by the heap, with the same operation.
Implementation of Max Binary Heap
The index of the left-child of each node is i * 2 + 1, while the right's is i * 2 + 2, and the parent's is (i - 1) / 2
There are two central operations in the heap, shiftUp and shiftDown. The former is used for insertion, and the latter is to delete the root node.
The key of shiftUp is to compare with the parent node bubbly and exchange the position if it is larger than the parent.
As for shiftDown, first exchange root and the tail node, and then delete the tail. After that, Compare with the parent node and both child-nodes circularly, if the child-node is larger, assign the parent node with the larger node.

js
class MaxHeap {
constructor() {
this.heap = []
}
size() {
return this.heap.length
}
empty() {
return this.size() == 0
}
add(item) {
this.heap.push(item)
this._shiftUp(this.size() - 1)
}
removeMax() {
this._shiftDown(0)
}
getParentIndex(k) {
return parseInt((k - 1) / 2)
}
getLeftIndex(k) {
return k * 2 + 1
}
_shiftUp(k) {
// exchange if the current node is bigger than the parent node
while (this.heap[k] > this.heap[this.getParentIndex(k)]) {
this._swap(k, this.getParentIndex(k))
// update the index to the parent node's
k = this.getParentIndex(k)
}
}
_shiftDown(k) {
// exchange the head and tail, then delete the tail
this._swap(k, this.size() - 1)
this.heap.splice(this.size() - 1, 1)
// check whether the node has left child-node,
// the right must exist because of full-tree
while (this.getLeftIndex(k) < this.size()) {
let j = this.getLeftIndex(k)
// check whether the right child exits, and whether it is largger than the left
if (j + 1 < this.size() && this.heap[j + 1] > this.heap[j]) j++
// check whether the parenet node is largger than both child-nodes
if (this.heap[k] >= this.heap[j]) break
this._swap(k, j)
k = j
}
}
_swap(left, right) {
let rightValue = this.heap[right]
this.heap[right] = this.heap[left]
this.heap[left] = rightValue
}
}js
class MaxHeap {
constructor() {
this.heap = []
}
size() {
return this.heap.length
}
empty() {
return this.size() == 0
}
add(item) {
this.heap.push(item)
this._shiftUp(this.size() - 1)
}
removeMax() {
this._shiftDown(0)
}
getParentIndex(k) {
return parseInt((k - 1) / 2)
}
getLeftIndex(k) {
return k * 2 + 1
}
_shiftUp(k) {
// exchange if the current node is bigger than the parent node
while (this.heap[k] > this.heap[this.getParentIndex(k)]) {
this._swap(k, this.getParentIndex(k))
// update the index to the parent node's
k = this.getParentIndex(k)
}
}
_shiftDown(k) {
// exchange the head and delete the tail
this._swap(k, this.size() - 1)
this.heap.splice(this.size() - 1, 1)
// check if the node has left child-node, the right must exist if true according to the binary heap
while (this.getLeftIndex(k) < this.size()) {
let j = this.getLeftIndex(k)
// check if the right child exits, and whether it is largger than the left
if (j + 1 < this.size() && this.heap[j + 1] > this.heap[j]) j++
// check if the parenet node is largger than both child-nodes
if (this.heap[k] >= this.heap[j]) break
this._swap(k, j)
k = j
}
}
_swap(left, right) {
let rightValue = this.heap[right]
this.heap[right] = this.heap[left]
this.heap[left] = rightValue
}
}