Appearance
排序是很常见也很经典的问题,下面讲几种排序算法:
冒泡排序
冒泡排序是最好理解的一种算法,以升序排序为例,即最小的在前面,对数组进行一次遍历,如果相邻的两个数前面的比后面的大,则交换他们的位置,第一次遍历会将最大的数字排到最后去,第二次遍历会将第二大的数字排到倒数第二的位置。。。以此类推,遍历n-1遍整个数组就有序了。详细解说参考https://www.runoob.com/w3cnote/bubble-sort.html:
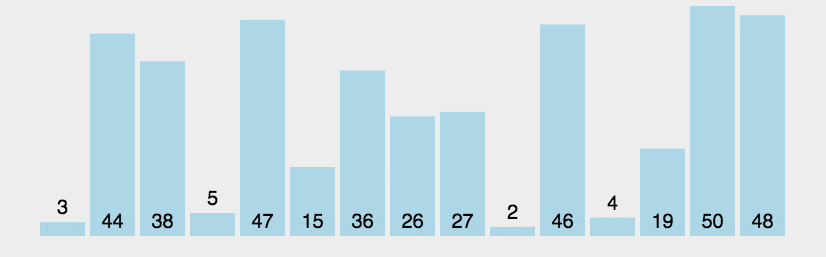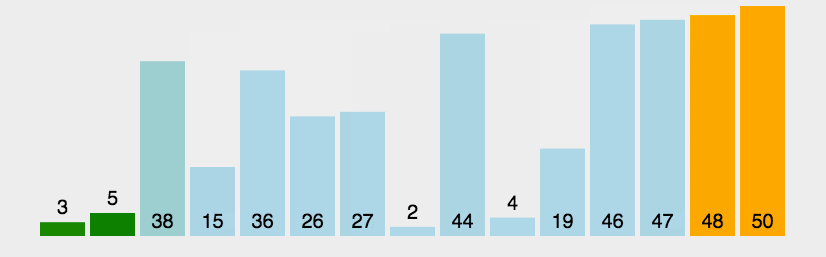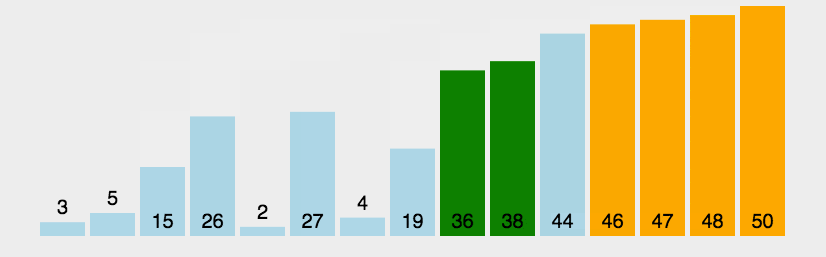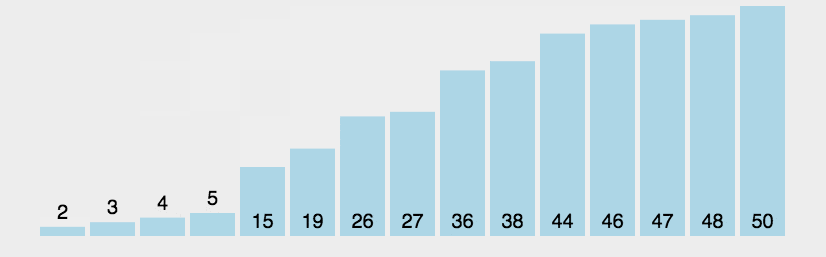
下面我们自己来实现一遍代码:
javascript
const array = [1, 3, 2, 6, 4, 5, 9, 8, 7];
const sort = (arr) => {
let result = [...arr];
let temp;
for(let i = 0; i < result.length - 1; i++){
for(let j = 0; j < result.length - 1 -i; j++){
if(result[j] > result[j + 1]){
temp = result[j];
result[j] = result[j + 1];
result[j + 1] = temp;
}
}
}
return result;
}
const newArr = sort(array);
console.log(newArr); // [1, 2, 3, 4, 5, 6, 7, 8, 9]插入排序
会打扑克的同学应该很熟悉这个排序法,每次摸牌的时候都去手里面已经排好序的牌里面比较下,找到它的位置,插入进去。这个查找可以使用二分查找,所以更快。具体分析看这里:https://www.runoob.com/w3cnote/insertion-sort.html
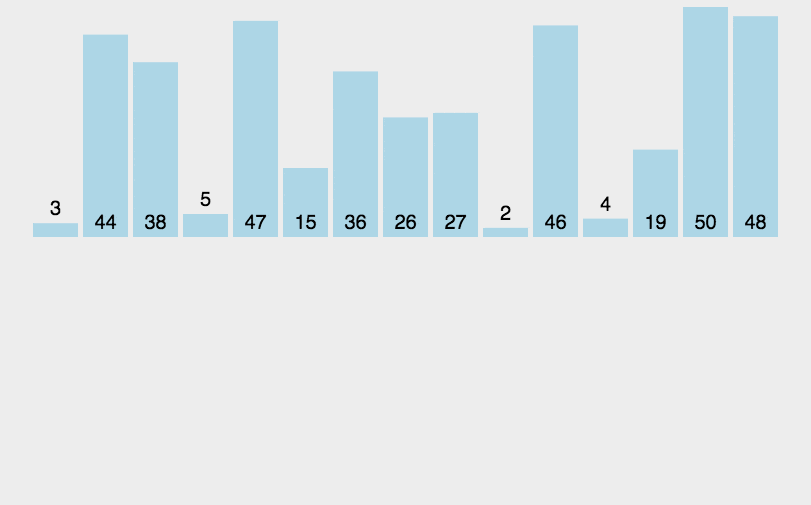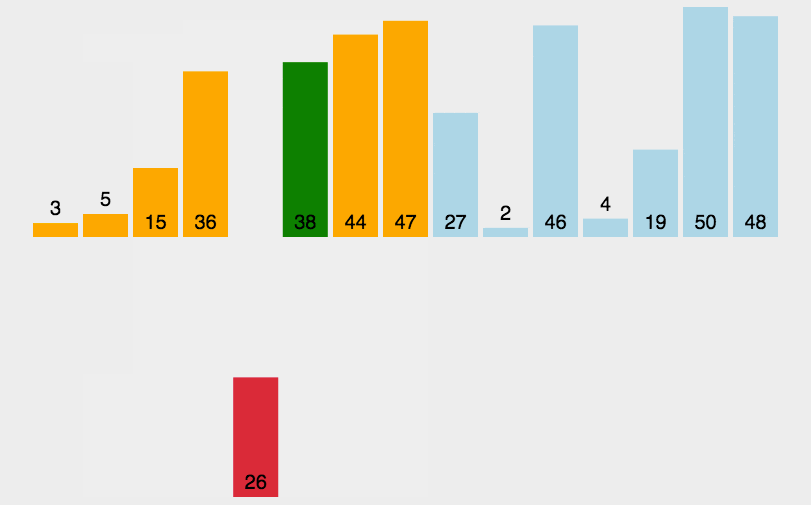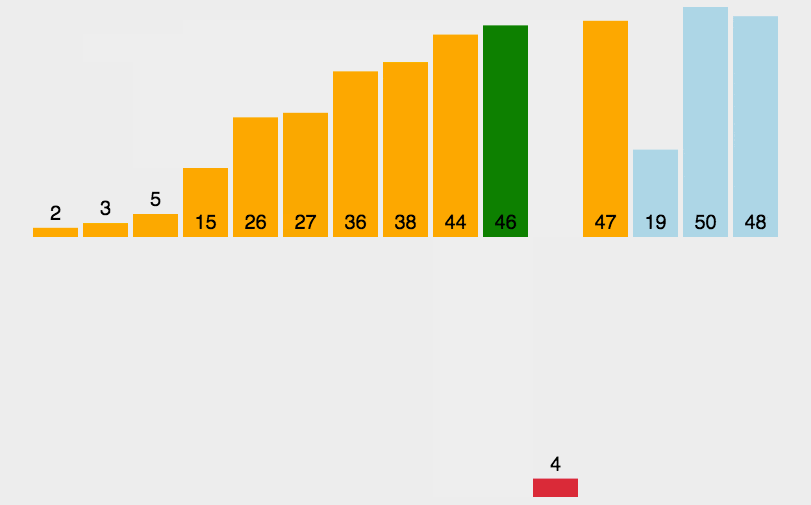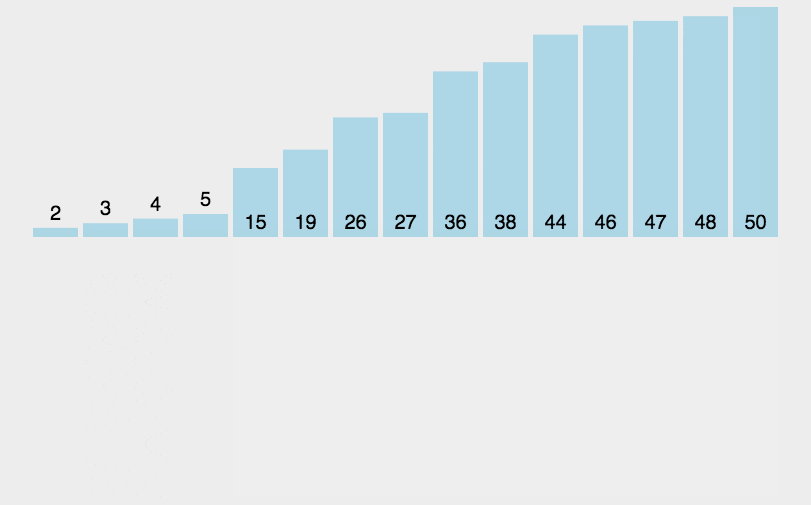
javascript
const array = [1, 3, 2, 6, 4, 5, 9, 8, 7];
const sort = (arr) => {
let result = [...arr];
let temp;
for(let i = 0; i < result.length; i++){
let j = i;
while(result[j - 1] > result[j] && j>=0){
temp = result[j - 1];
result[j - 1] = result[j];
result[j] = temp;
j--;
}
}
return result;
}
const newArr = sort(array);
console.log(newArr); // [1, 2, 3, 4, 5, 6, 7, 8, 9]javascript
// 二分查找版
const array = [1, 3, 2, 6, 4, 5, 9, 8, 7];
const sort = (arr) => {
let result = [...arr];
let i = 0;
let length = result.length;
for(i; i < length; i++) {
let left = 0;
let right = i - 1;
let current = result[i];
// 找目标位置, 最终的left就是目标位置
while(left <= right) {
let middle = parseInt((left + right) / 2);
if(current < result[middle]){
right = middle - 1
} else {
left = middle + 1;
}
}
// 将目标位置后面的元素全部后移一个,位置让出来
for(let j = i - 1; j >= left; j--){
result[j+1] = result[j];
}
// 最后将当前值插入到正确位置
result[left] = current;
}
return result;
}
const newArr = sort(array);
console.log(newArr); // [1, 2, 3, 4, 5, 6, 7, 8, 9]快速排序
快速排序是一个效率很高而且面试中经常出现的排序,他的平均时间复杂度是$$O(nlogn)$$,最差时间复杂度是$$O(n^2)$$。他的核心思想是选定一个基准值x,将比x小的值放到左边,比x大的值放到右边。假设我们有如下数组:
javascript
const a = [3, 6, 2, 1, 4, 5, 9, 8, 7];我们每次都取数组的第一个值为x,然后将比他小的放到左边,大的放到右边。这里我们的第一个值3,经过这么一次运算后,我们期望的目标是得到类似这样一个数组:
javascript
const a = [2, 1, 3, 6, 4, 5, 9, 8, 7];注意这个数组,3左边的都比3小,3右边的都比3大,左右两边里面的顺序可能是不对的,但是3本身的位置是对的。怎么来实现这个呢?我们用x把3暂存下来,然后使用两个指针i,j分别指向数组最开始和最后面。初始状态x = 3, i = 0, j = 8。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 3 | 6 | 2 | 1 | 4 | 5 | 9 | 8 | 7 |
我们暂存了a[0],就相当于把a[0]挖出来了,需要找一个数填进去。我们从后往前找,找一个比3小的数,我们发现a[3]是1(j=3),比3小,将它填到a[0]的坑里。注意,这时候i=0, j=3。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 2 | 1 | 4 | 5 | 9 | 8 | 7 |
a[3]被填到了a[0]的位置,相当于a[3]又被挖出来了,又需要找一个数来填充。这次我们从前往后找,找一个比x大的数,我们发现a[1]是6(i=1),比x大,将它填到a[3]的位置。注意,这时候i=1, j=3。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 2 | 6 | 4 | 5 | 9 | 8 | 7 |
这时候a[1]被填到了a[3]的位置,相当于a[1]又被挖出来了,又可以继续填充数字,我们继续从j的位置往前找一个小的。我们发现a[2]比3小,我们将a[2]填充到a[1]的位置。注意,这时候i=1, j=2;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 6 | 4 | 5 | 9 | 8 | 7 |
a[2]填充到了a[1],a[2]又空了,我们继续从前往后找一个大的数字填充进去,i开始自增,但是他自增一个之后就不小于j了。这说明我们整个数组已经遍历完了,循环结束。注意,i自增一次后不小于j,触发循环结束条件,此时i = 2。 而这时候的i就是我们最开始缓存的x应该在的位置,我们将x放入a[i]。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 6 | 4 | 5 | 9 | 8 | 7 |
至此,一次遍历就找到了基准值应该在的位置,并且调整了数组,让基准值左边的数都比他小,右边的都比他大。我们来实现下这个方法。
javascript
const partition = (arr) => {
let x = arr[0];
let length = arr.length;
let i = 0;
let j = length - 1;
while(i < j) {
// 先从后往前找小的, 没找到继续找
while(i < j && arr[j] > x) {
j--;
}
// 找到了,将值填入坑里, a[j]又变成了坑
if(i < j) {
a[i] = a[j];
}
// 然后从前往后找大的,没找到继续找
while(i < j && arr[i] < x) {
i++;
}
// 找到了,将值填入之前的坑里
if(i < j) {
a[j] = a[i];
}
}
// 将基准值填入坑
a[i] = x;
return arr;
}
const a = [2, 1, 3, 6, 4, 5, 9, 8, 7];
// 测试下
let result = partition(a);
console.log(result); // [1, 2, 3, 6, 4, 5, 9, 8, 7]在前面思路的基础上继续递归的对基准值左右两边调用这个调整方法,就能将数组的每个数字都放到正确的位置上,这就是快速排序,这种思想叫分治法。前面调整数组的方法我们需要进行微调,让他接受开始位置和结束位置并返回基准值的位置。
javascript
const partition = (arr, left, right) => {
let x = arr[left];
let i = left;
let j = right;
while(i < j) {
// 先从后往前找小的, 没找到继续找
while(i < j && arr[j] > x) {
j--;
}
// 找到了,将值填入坑里, a[j]又变成了坑
if(i < j) {
a[i] = a[j];
}
// 然后从前往后找大的,没找到继续找
while(i < j && arr[i] < x) {
i++;
}
// 找到了,将值填入之前的坑里
if(i < j) {
a[j] = a[i];
}
}
// 将基准值填入坑
a[i] = x;
return i;
}
const quickSort = (arr, left, right) => {
const length = arr.length;
const start = left || 0;
const end = right !== undefined ? right : length - 1;
if(start < end) {
const index = partition(arr, start, end);
quickSort(arr, start, index - 1); // 调整基准值左边
quickSort(arr, index + 1, end); // 调整基准值右边
}
return arr;
}
const a = [2, 1, 3, 6, 4, 5, 9, 8, 7];
// 测试下
let result = quickSort(a);
console.log(result); // [1, 2, 3, 4, 5, 6, 7, 8, 9]归并排序
归并排序比快速排序好理解,时间复杂度也是$$O(nlogn)$$,采用的思想也是分治法。假设我们已经有两个有序数组。
javascript
const a = [1 ,2, 6, 8];
const b = [3, 4, 9];我们现在写一个方法来得到a跟b组合后的有序数组,这个方法很简单,用两个指针i,j分别指向两个数组,然后开始遍历,比较a[i]和a[j]的大小,将小的那个放入新的有序数组。当任意一个数组遍历完,循环结束,将剩下的值全部放入新的有序数组:
javascript
const merge = (arr1, arr2) => {
const length1 = arr1.length;
const length2 = arr2.length;
const newArr = [];
let i = 0;
let j = 0;
while(i < length1 && j < length2) {
if(arr1[i] <= arr2[j]) {
newArr.push(arr1[i]);
i++;
} else {
newArr.push(arr2[j]);
j++;
}
}
// arr2还剩一些
if(i === length1 && j < length2) {
while(j < length2) {
newArr.push(arr2[j]);
j++;
}
}
// arr1还剩一些
if(j === length2 && i < length1) {
while(i < length1) {
newArr.push(arr1[i]);
i++;
}
}
return newArr;
}
// 测试一下
const a = [1 ,2, 6, 8];
const b = [3, 4, 9];
const result = merge(a, b);
console.log(result); // [1, 2, 3, 4, 6, 8, 9]然后我们递归的将待排序数组分成左右两个数组,一直分到数组只含有一个元素为止,因为数组只含有一个元素,我们就可以认为他是有序的。
javascript
const mergeSort = (arr) => {
const length = arr.length;
if(length <= 1) {
return arr;
}
const middle = Math.floor(length / 2);
const left = arr.slice(0, middle);
const right = arr.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
// 测试一下
const a = [2, 1, 3, 6, 4, 5, 9, 8, 7];
// 测试下
let result = mergeSort(a);
console.log(result); // [1, 2, 3, 4, 5, 6, 7, 8, 9]